Problem: We have a file (or a set of files) and we want to search for all email IDs present within those files. The email IDs may be embedded within sentences and may be found anywhere in the file. We have a set of rules that specify what constitutes a valid email ID.
As we shall see, the solution we will discover will be quite generic and will solve a whole class of search / replace problems, not just this.

Solution 1:

Usually, we take this opportunity to describe a naive solution to the problem. Here, I will describe an approach briefly and then move on.
One way to solve the problem is to come up with some procedural logic that will scan each character in the input file(s) and check it to see if it can be a part of an email ID. Basically, it will search for an '@' sign and look to its left and right to decide. However, any such solution has to be more than say, 60 lines long piece of code. Let's try something different.

Solution 2:

Regular Expressions are used very widely for search / replace and other problems. Mastering even the basics of regular expressions will allow you to manipulate text with surprising ease.
Before starting, let us define the terms we will use often in this text. A set is an unordered collection of distinct elements having specific common properties. For example, the set of positive integers, {0,1,2,3,...}. A string is a linear sequence of elements from the set.
A regular expression (or regexp, or pattern, or RE) is a text string that describes some (mathematical) set of strings. A RE r matches a string s if s is in the set of strings described by r.

Using a RE library, you basically can:

• see if a string matches a specified pattern as a whole, and
• search within a string for a substring matching as a specified pattern.

I will not try to give a comprehensive account of their syntax. For that, I refer readers to Perl information sites, regular expression whitepapers on the net, or the documentation for your particular regular expression library. Indeed, regular expressions come in many different flavours, each differing from the other in syntax, capabilities and the implementation method. This paper is too small to cover regular expressions in their entirety. For that, I refer you to Mastering Regular Expressions by Jeffrey E.F. Friedl. The purpose of this document is to associate regular expressions with ordinary problems in software development and encouraging their use.

Regular Expressions have their own notation. Characters are single letters for example ‘a’, ‘ ’ (single blank space), ‘1’ and ‘-’ (hyphen). Operators are entries in a RE that match one or more characters. You compose REs by combining operators. Theory of computation literature uses the operators listed in Table 1.

Suppose Σ={a,b}. The set Σ, containing the symbols a and b is known as alphabet. The set of all possible strings of symbols that can be written using symbols from this alphabet is called Kleene Closure. This is denoted by Σ*, informally meaning "the repetition of any symbol in Σ, zero or more times". The repetition of any symbol in Σ one or more times is written as Σ+ and is known as the set's positive closure.
So, using closures, we can see that the strings containing only as can be denoted by a* or (Σ-b)*. Strings starting with a can likewise be denoted by aΣ^*. All these, that is Σ^*, a* and (Σ-b)* are regular expressions. At times, we draw diagrams for these called finite automata. For Σ^*, the diagram would be like the one show in Figure 1.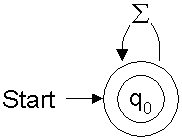

Figure 1: Finite automaton for Σ^*

We always start at the marked state (q0 in this case), keep moving through the arrows using up one character each time we move through an arrow. We follow the arrow that matches the current input character. If we end up at a state that has a double circle, the input is accepted (as having matched). Here, on matching any character, the state remains q₀, which is also a final state hence any string of characters matches this regular expression.

Let's see another example. For aΣ^*, the finite automaton is shown in Figure 2.

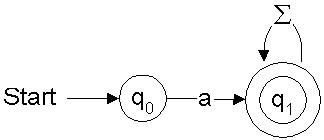
Figure 2: Finite automaton for aΣ^*

This means, we start at q0. If the first character in the input is a, we move to q1 and remain there until all the letters in the input are exhausted. Since we end on state q1 (which has a double circle,indicating that its a final state), the string belongs to aΣ^*. If the first character is not a, we stay at q0, hence the string is not accepted. More on this later.

However, language implementations use slightly modified notation. A small list appears in Table 2.

All libraries may not allow all of above operators. In addition, some notation has caught on from Unix, as shown in Table 3.

So, instead of using [a-zA-Z_0-9]+ to match a word, simply use \w+. \b is a zero-length operator that checks for word boundary (change from \s to \w or reverse) without matching anything. To match hard in 'Hard steel is expensive.' but not 'Hardworking people are in demand', use Hard\b. Some examples of use of regular expressions are given in Table 5.

Now that we have seen what regular expressions are, let us see what they can be used for. There are four possible uses of regular expressions:

1. Searching:
   
   Let us say we want to search for all numbers within a character string. An example of the character string is:
   
   
   abcdaef12345fghfgh234eioutsrkplmn
   
   
   In this string, 12345 and 234 are to be extracted.
   To solve this problem, we need to search within the string using the regular expression [0123456789]+ or [0-9]+. I will give a code sample on how to do such searches using REs in Java later, while discussing the solution to the problem given at the beginning of this text.
   
   
2. Replacing:
   
   Let us say we have some text having numbers with some numbers wrongly written as .123, instead of 0.123. Let us say we want to correct these. We can use the regular expression ([^0-9])(\.[0-9]+) (or, in short, (\D)(\.\d+)). The meaning of this RE is explained in Table 6.
   Table 6

   Part of RE	Significance
   [^0-9]	starts with a non-digit character
   (...)	work as capturing group; explained later
   \.	has a dot. The backslash signifies that we are using a dot as a normal character; not to match 'any character from the alphabet'
   [0-9]+	has any number of digits afterwards (at least one is required)

   The part within parenthesis has a special meaning within regular expressions. It can be used to remember (store) the part of the pattern that was matched by that part of the RE. For example, if we use (.)([0-9]) and it matches A1, then A is remembered as the first capture group and 1 is remembered as the second capture group. The capture groups are then accessible through variables or function calls (depending on the library in use). In Perl, this can be accessed through the $1 variable for the first group within parenthesis, $2 for the next pair of parenthesis and so on. $& is always the completely matched string, that matches the whole expression. In Java, there are functions to access these groups depending on the library used. So, using the RE library, we now have to replace the string found with $10$2, where $1 would contain the non-digit character found and $2 the digits and decimal point. (With some RE engines, $10$2 might be interpreted to mean the text of the tenth capture group, followed by the second. In such case, you might have to rephrase this as concatenation: $1 . "0" . $2.)
   Since this is a widely used application of regular expressions, let's do another example.
   We have a file pathname something like "C:\Windows\desktop\abc.txt" (not including the quotes) and we need to extract only the filename, "abc.txt". If we use normal procedural logic, we would have to scan the string from the end, looking for a backslash and then create a new string copying from that index to the end. Instead, using REs, it boils down to just a single line:
   (here I use C# RE syntax; it is similar for other languages)
   
   string text = @"C:\Windows\desktop\abc.txt";
string pattern = @"^.*\\";
string result = Regex.Replace(text,pattern,"");

The RE ^.*\\ means "start at the beginning and go on looking until you find a '\' (the double backslash means that '\' is being used as a character, not as regular expression operator)". Now a question arises, as to which backslash sign the \\ operator will match - the first one, the last one or the one in the middle? If it matches, for example, the first one, the final result after the replacement will be 'Windows\desktop\abc.txt' and not what we want.
   In truth, the + and the * operators are greedy - they like to absorb as many characters as possible, unless forced by an overall match criteria to give up characters. For example, consider the RE .*er. The .* can match b or berib in beriberi. However, because the * operator is greedy, it will match berib.
   Hence in this case, the backslash that matches will always be the last one. The Replace statement then causes the matched part to be replaced by a blank, effectively deleting it from the string. Finally, the string 'result' will contain the filename 'abc.txt'.
   It is also important to understand when a RE will give up its greed to allow an overall match. Consider the RE t.*[0-9]a and the pattern txb9axxxa. In this particular case, the RE will match the first a, the overall match being txb9a since the second a does not have a digit before it.
   
   
3. Parsing:
   Parsing means taking apart in order to process some input. Dictionary meaning being "to analyse (a string of characters) in order to associate groups of characters with the syntactic units of underlying grammer." Let us say, we have a typical URL:
   

   http	://	www.xyz.com	/doc/public	/xxx.html
   1		2	3	4

   In this, -1- is a protocol, -2- is the name of a server, -3- is a path and -4- is the name of a document. Suppose we want to write a program that takes a URL and returns the protocol used, the DNS name of the server, the directory and the document name. We can do this using a RE as:
   
   
   ^(ftp|http|file)://([^/]+)(/.*)?(/.*)
   
   
   It says, start at the beginning, look for a protocol (one of ftp, http or file as denoted by ftp|http|file), look for ://. This part is parenthesised to denote that the protocol used should be remembered, and be available through variables later. Next, look for DNS name (as in ([^/]+)), then for an optional path (as denoted by the question mark after (/.*)?) and thereafter, for a document name (/.*). Convince yourself that the regular expression will do what is required and remember the four required values as $1, $2, $3 and $4(in Perl).
   
   Let us say, we enter the URL given above. The values returned are:
   $1 = http
$2 = www.xyz.com
$3 = /doc/public
$4 = /xxx.html

   If we enter a URL that does not have a path, like,
   http://www.xyz.com/a.html
   
   
   the RE still works (because of the question mark) and returns:
   $1 = http
$2 = www.xyz.com
$3 = null
$4 = /a.html

   
   
   Or, if the document is also not given, as in,
   
   
   http://www.xyz.com/
   
   
   then $4 contains just the slash. Note that this regular expression works only on VALID inputs. If the URL entered is invalid, it churns out invalid results (a case of GIGO). I leave to the reader as an exercise to write a RE that validates and parses the URL at the same time.
   
   
4. Validation:
   
   We discuss the age old problem of date validation. A date is something like 23/4/2002 or 23-04-2002. For the day part, ([0-3]{0,1}[0-9]) would suffice. That is, an optional 0/1/2/3 followed by a digit. Instead of [0-3]{0,1}, we could also have used [0-3]?. Now, say, we want to allow both dash(-) separated and slash(/) separated dates. So, we write the next part as: /([01]{0,1}[0-9])/ or \-([01]{0,1}[0-9])\- (the slash indicates that the '-' is being used literally, not as RE notation). Please note that I have put a slash at the start and end instead of having [/\-]([01]{0,1}[0-9])[/\-]. This is to ensure that dates like 21-3/97 are not accepted. Similarly, RE for the year is written. The full expression is given in the procedure below. Instead of using (...), we use (?:...) when we want a part of the expression to be clubbed, but do not want the part that matched that within the parenthesis to be remembered. For example, instead of writing housecat|housekeeper, we can say house(?:cat|keeper). Here, the parenthesis is only for easy organization (or for use with * and + operators), not as capture group. The procedure is given in Listing 1. In order to compile this, gnuregexp.jar [hosted here with permission from Wes Biggs, and licensed under GNU LGPL] needs to be in the CLASSPATH, and gnu.regexp.* library needs to be imported. In addition, java.util.* needs to be imported for Date.

   /* Listing 1. This uses GNU Regexp library to parse dates */
   /* All rights reserved. Copyright Hardeep Singh 2002      */
   /* http://www.SeeingWithC.org/topic7html.html             */
   public Date parse(String date)
   {
           String strRe=new String("([0-3]{0,1}[0-9])" +
                                   "(?:(?:/([01]{0,1}[0-9])/)" +
                                   "|(?:\\-([01]{0,1}[0-9])\\-))" +
                                   "((?:19|20)[0-9]{2})");
                                        // the regular expression
           RE exp=null;
           try {
                   exp = new RE(strRe); // create a regular expression
           }
           catch (REException e) {
           	// cannot happen for this regexp
           }
           REMatch rem=exp.getMatch(date);
                                        // see if matches
           if (rem!=null) 	{
                   int dd,mm,yyyy;
                   String tempMm;
                   try {
                           dd=Integer.parseInt(rem.toString(1));
                                        // get the first capture group value
                           tempMm=rem.toString(2);
                                        // second and third
                                        // only one of second and third is
                                        // valid, and that is the month
                           if (tempMm.equals(""))
                                   mm=Integer.parseInt(rem.toString(3));
                           else
                                   mm=Integer.parseInt(tempMm);
                                        // fourth
                           yyyy=Integer.parseInt(rem.toString(4));
                   }
                   catch (NumberFormatException nfe) {
                           return null;
                   }
                   Calendar cal = new GregorianCalendar();
                                        // create the date object and return
                   cal.set(yyyy,mm-1,dd);
                   return cal.getTime();
           }
           else
                   return null;
   }
   

Note that certain improvements are in order. For example, the RE allows day-of-month to be 39. Although, such values are rejected later during processing, we can change the day part to [0-2]{0,1}[0-9]|30|31. Similarly, the other parts can be made stricter, for example the month part can be changed to exclude months like 00 or 19. These changes are left to the reader.
This procedure runs only five times slower than an equivalent that does not use regular expressions. Moreover, with newer approaches to regular expression optimisations being developed, the time difference will reduce even further.

Having seen regular expressions being used, let us turn our attention to how they work. That is, how is a RE engine (as part of a RE library) able to accept or reject strings? There are two approaches:

1. DFA approach
2. Procedural approach

Let us understand these.

DFA approach:
Somewhere in the beginning of this text, I showed you finite automata diagrams. For every RE, we can construct a Deterministic Finite Automata (DFA) and vice-versa. A DFA is nothing but a kind of program to find out if the RE matches some text or not. This kind of engine first constructs a Non-Deterministic Finite Automata (NFA) equivalent to the RE. From this NFA, it constructs a DFA equivalent and executes the DFA on the input string.
Let us do an example on this. We want to detect all strings containing only as and bs and ending with abb. We present the regular expression (a|b)*abb$ to the engine. It constructs an NFA as shown in Figure 3.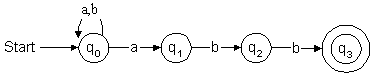

Figure 3: Non-deterministic finite automata

However, the computer cannot execute this directly because it cannot decide between moving to q1 and staying at q0 when it encounters an a at q0. Hence, the computer translates this into the DFA as per Figure 4.

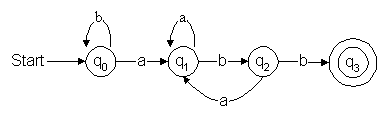
Figure 4: Deterministic finite automata

This can be easily executed. The way this done for input string abaababb is in Table 7.

Table 7

Input absorbed	State
-	q0
a	q1
b	q2
a	q1
a	q1
b	q2
a	q1
b	q2
b

We have a match whenever the state reaches q3.

Procedural approach:
This approach uses a procedure to decide if the input matches or not. Let us say it has to match a string to (a|b)*abb. First, it will match the first character (say, a) with the expression. (a|b)* accepts that. Similarly matching, it goes to the end of the input string matching the as or bs, and with (a|b)* accepting all. Now, it sees the abb part of the RE and decides to back off in the input string until it has found an a, then looks for bs after it and so on. Sometimes, this approach is also called NFA approach (because it is 'opposed' to DFA approach) but since it does not actually use a NFA, I do not like to call it by that name.
The advantage of DFA approach is that it is very fast. Most of the time, the speed difference is small. However, if the RE is something like (a|b+)* (that is, the RE contains nested quantifiers; which we should anyway avoid), the difference can be huge, especially if the pattern does not match (because all possibilities will be tried before giving up). Also, if a RE has to match multiple times (as for example searching for matches in a set of files), the saving can be significant.
However, the Procedural approach is easier to implement and can provide more features than DFA approach. For example, it is not easy to implement capture groups (using parenthesis within RE, as shown) in DFA approach. The Unix 'Awk' tool uses DFA approach while Perl uses Procedural approach. However, these days most tools use a mixed logic to do the matching. They might use DFA approach to check if a match is there, and then use Procedural approach to get the values of capture groups. Some newer DFA implementations also support capture groups.
However, there is one more key difference in the two approaches. Sometimes, the same regular expression can be rearranged to produce different results with a Procedural engine. Consider the RE t(e|es). and the input string test. A DFA based engine will always give the matched string as test, but the Procedural engine will beg to differ. It will analyse the (e|es) part and will consider the e first. That is, it will logically look at the RE first as te. and will match tes, not test. Since there is a match, the engine will never backtrack and consider the other option es. Had there been no overall match, it would have considered matching es, seen the RE as tes. and matched test. If the RE is rearranged to t(es|e)., the Procedural engine would also match test. The DFA engine always returns the longest match possible. Period.

Now, we come to the solution to the discussed problem. I will give a Java program as an answer and it will use RE library built into JDK1.4. However, the program can be made to run on any Java version using other libraries with minimal changes. The RE we use is something like:

[a-z0-9\.\-\_]+@([a-z0-9\-\_]+\.)+(com|net|[a-z]{2})

Since we are using a case insensitive match, we do not need to add A-Z. Also, in the actual program, we include all other possible domain names ORed with COM and NET. To allow country codes like IN for India, US for USA etc., we use [a-z]{2}. Convince yourself that the rest of the expression is correct. The program is shown in Listing 2.

// Listing 2. Uses RE to detect email IDs in files
// Requires Java 1.4 or above
/* All rights reserved. Copyright Hardeep Singh 2002      */
/* http://www.SeeingWithC.org/topic7html.html             */
import java.util.regex.*;
import java.io.*;

public class Emails {

	public static void main(String args[]) {
		if (args.length < 1) {
			System.out.println("USAGE: java Emails filename [-comma]");
			System.exit(1);
		}

		String strRe=new String("[a-z0-9.\\-_]+@([a-z0-9\\-_]+\\.)+(" +
					"com|net|org|edu|int|mil|gov|arpa|biz|" +
					"aero|name|coop|info|pro|museum|tv|([a-z]{2}))");
				// the regular expression
				// 'tv' can be omitted because it is
				// covered under [a-z]{2}

		Pattern p = Pattern.compile(strRe,Pattern.CASE_INSENSITIVE |
		                            Pattern.UNICODE_CASE | Pattern.MULTILINE);
				// compile it

		String content=null;
				// read the input file into content
		boolean comma=false;
		try {
			FileInputStream fin=new FileInputStream(args[0]);
			StringBuffer sb=new StringBuffer();
			int ch;
			while ((ch=fin.read())!=-1)
				sb.append((char)ch);
			fin.close();
			content=new String(sb);
		}
		catch (Exception e) {
			System.out.println("Cant read file.");
			System.exit(1);
		}

		if (args.length>=2) {
			if (args[1].equalsIgnoreCase("-comma"))
				comma=true;
		}

		boolean theEnd = false, printed = false;
		Matcher m = p.matcher(content);
				// get the results and print

		while (!theEnd) {
			theEnd = !m.find();
			if (!theEnd) {
				if (comma)
					if (!printed)
						System.out.print(content.substring(
						                 m.start(),m.end()));
					else
						System.out.print(", "+content.substring(
						                      m.start(),m.end()));
				else
					System.out.println(content.substring(
					                              m.start(),m.end()));
				printed=true;
			}
		}
	}
}

For those who do not have access to Java or RE library, I also present an Awk program for the same purpose. It can be invoked as awk -f email.awk <filename> where email.awk contains the following program and <filename> is the name of file in which to search for email IDs.

# All rights reserved. Copyright Hardeep Singh 2002      #
# http://www.SeeingWithC.org/topic7html.html             #
{
        r="[a-z0-9\\.\\-\\_]+@(([a-z0-9\\-\\_])+\\.)+(com|net|org|edu|int|mil|gov" \
                              "|arpa|biz|aero|name|coop|info|pro|museum|tv|[a-z][a-z])";
        a=$0;
        while (length(a)!=0) {
        	if (match(toupper(a),toupper(r))) {
        		print substr(a,RSTART,RLENGTH);
        	}
        	else
        		break;
        	a=substr(a,RSTART+RLENGTH,length(a));
        }
}

Now, we come to irregular expressions. Throughout the text, we have been saying "regular expressions". You might have been wondering if there is also something called irregular expressions. Well, there is. As an example, the set:

{anbn: n>0, an means a repeated n times}

That is, the set of all strings like {ab,aabb,aaabbb,...} (having the same no of bs following some number of as). This is irregular in the sense that all the members cannot be represented by a DFA based RE, that is one without using advanced features like capture groups. However, using a set of RE operations and capture groups, we can still match members of this set. While discussing the solution, I will uncover one more feature of REs.

Backreferences are used within REs to refer to "what has already been matched". A backreference matches a specified preceding group. The backreference operator is represented by \digit. However, this is not supported by all RE libraries. The notation used is \1 for the 1st capture group, \2 for the second and so on. Say, we want to match strings of the form x@x where x is a string. That is, aaa@aaa is valid but not aaa@bbb. The RE for this is (.*)@\1. This means, anything before the @ is stored as first capture group (accessible in Perl through $1, as discussed) and that same thing should be repeated after the @ (indicated by \1). If the group matches a substring, the backreference matches an identical substring. If the group matches more than once (as it might if followed by, e.g., a repetition operator), then the backreference matches the substring the group last matched. We would use this feature to accept (or reject) strings of the form anbn. However, we cannot use backreferences directly such as (a+)\1 because we need to match bs in the second half instead of as in the first. Hence, we must somehow transform the input so that it can be validated. Here, we make this transformation:

1. Replace an occurrence of ab in the input with axa.
2. Replace all bs with as.

Hence, on being given aabb, after the first transformation, it becomes aaxab and after second, aaxaa. Both these transformations are done through REs. Now, we can simply check using the RE ^(a+)x\1$. A complete JavaScript function to check such strings forms all of Listing 4.

// Listing 4
// Javascript function to test if
// a^nb^n (n>0) is irregular
// Which means the set containing strings having any number
// of a's followed by the same number of b's cannot be
// represented by a single regular expression. Here we try to
// do it through two regular expressions without using any
// programming logic
/* All rights reserved. Copyright Hardeep Singh 2002      */
/* http://www.SeeingWithC.org/topic7html.html             */
function doValidate(id)
{
        var reg1,reg2,reg3;
        reg1 = /ab/;
        reg2 = /b/g;
        reg3 = /^(a+)x\1$/;

        if (reg3.test(id)) {            // this test is important
                alert("Invalid.");      // if the expression is of the
                return;                 // form a^n.x.a^n right from
        }                               // the start, then it will match.

        id = id.replace(reg1,"axa");

        id = id.replace(reg2,"a");
        // now the expression is of the form a^n.x.a^n, which is regular

        if (reg3.test(id))
                alert("Valid.");
        else
                alert("Invalid.");
}

Before concluding, I will talk about one additional simple yet powerful approach that can simplify code - lookup tables. This approach was pioneered by Greg Ubben for a Unix tool called sed, but can be used in any regexp tool.

Assume that we created a school report, containing roll numbers instead of names for a class of forty students. The report goes something like this:
"... The award for the highest attendence goes to 03, who also has credit for best handwriting sharing it with 10..."

Now in this text, we want to replace all numbers with names. One way to accomplish this is to run forty search/replace commands. Instead, let us say, we want to do this in fewer searches. We split the students into four groups, of ten students each (for manageability). In the first group are students from roll number 1 to 10. We create a lookup table like this:

01Sam02Paul03Becky04Andy05Dick06Phillip07Cheryl08Susan09Harry10Faby

Next, we append it to each line in the pattern with the hash sign as separator:
The award for highest attendance goes to 01#01Sam02Paul03Becky04Andy05Dick06Phillip07Cheryl08Susan09Harry10Faby

Now we use the RE searching facility for \([0-9][0-9]\)\(.*\)#\(.*\)\1\([a-z]+\) and replacing with \4\2#\3\1\4. This will need to be done in a loop, until there are no further matches (since its possible to have more than one role number on a given line of text). This basically looks for a number in the first part of pattern (before the #) and when found, looks for the same number in the second part. Then it picks up letters after the second match and replaces suitably.
Finally, we remove the lookup table using replacement of #.* with "nothing".

The sed script to do this is below:

#append the lookup table to the input
s/$/#01Sam02Paul03Becky04Andy05Dick06Phillip07Cheryl08Susan09Harry10Faby/
:a #loop, looking for numbers and carry out the replacement
s/\([0-9][0-9]\)\(.*\)#\(.*\)\1\([a-zA-Z]\+\)/\4\2#\3\1\4/
ta #loop if match
#remove the lookup table
s/#.*//

Similarly, we would need to include additional commands for the other three groups, or use longer lookup tables. The script is more complex than anything we have seen so far. Please spend some time to understand it.

Conclusion
We saw that regular expressions provide us with an easy way to manipulate text. The operators +, * etc. can be employed to write REs with complex matching capabilities. REs can be used for searching, replacing, parsing and validating strings. REs can be DFA or procedure based, each of which has its own advantages and disadvantages. While a DFA based engine is faster, procedural engines provide more flexibility. REs are supported by many tools and languages. Even irregular matching requirements can be handled easily because of modern tools available.

Happy Regular Expression(ing)...